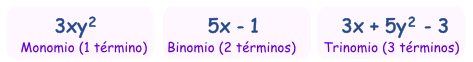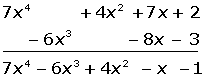“Ecuaciones lineales”
·
Ecuación:
es una igualdad matemática en la que intervienen variables,
pero la igualdad matemática entre dos expresiones se mantiene.
·
Incognitos
de la ecuación: Es una igualdad matemática en la que
intervienen variables, pero la igualdad matemática entre dos expresiones se
mantiene. (a, b, c, d, x, z, y, etc.)
·
Identidad:
es la igualdad que se verifica, es
decir, sólo es válida para ciertos valores de las incógnitas.
X+12=
16; si x=4
·
Conjunto
solución: conjunto de valores numéricos que cuando se sustituyen por el lugar
de las incógnitas da como resultado en una ecuación numérica (hacen válida la
ecuación).
·
Ecuaciones
equivalentes: Es una ecuación que tiene o produce otra
que tiene en común el resultado
4x-12=0
y 6x-12=0
“Soluciones de ecuaciones”
Resolver
una ecuación es el valor que debe de tomar una
variable para cumplir alguna condición dada.
Ø
Para
resolver las ecuaciones necesitamos reglas como:
1. La propiedad conmutativa: dice que
el orden los factores no altera el producto.
5+8=8+5
2. La propiedad asociativa: dice que
en una suma o multiplicación el orden de los factores no altera el producto
(2z)(3z)(4z)= 3z (2z)(4z)
3. La propiedad distributiva: de la multiplicación respecto a la suma (o la resta) es aquella por la que de dos o más números de una suma (o resta),
multiplicada por otro número, es igual a la suma (o resta) de la multiplicación
de cada término de la suma (o la resta) por el número.
6(2+3)= 6(2)+6(3)
4. los neutrales: son los números
especiales (0 y 1) entre los reales. El 0 es neutral en la suma y el 1 es
neutral en la multiplicación.
5+0=5 y
7x1=7
5. los contrarios: dice que para cada
número real positivo hay uno negativo.
6=-6
6. los recíprocos: es el número que
multiplicado por otro nos da como resultado 1.
“Ecuaciones
lineales con una incógnita”
Es aquella que puede
escribirse de esta forma: ax+b=0.
Donde “a” puede ser cualquier número diferente a 0. También reciben el nombre
de “ecuaciones de primer grado con una variable”
Ejemplos:
a)6x+8=20
6x=20-8
X=12/6
X=2
b)19-4x+4x= 3x+7+4x
4x=7-19
X=-12/4
X=-3

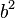 es menor que
es menor que  los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.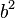 es mayor que
es mayor que  obtendremos dos valores distintos de X reales.
obtendremos dos valores distintos de X reales.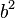 es igual que
es igual que  obtendremos dos valores de X reales e iguales.
obtendremos dos valores de X reales e iguales. se le llama discriminante
se le llama discriminante