Semana 3
Sistemas de ecuaciones lineales
3x3.
1)Lo primero que se hace es eliminar una
incógnita tomando de las tres ecuaciones para eso se usa el método de suma y
resta.
2)Se toma la tercera ecuación, la cual no
se utilizo en el paso anterior y con otra cualquiera se elimina la misma
incógnita.
3)Queda un sistema de ecuaciones de 2x2 y
se resuelve con el método que elijas
4)Se sustituyen los valores obtenidos de
las 2 incógnitas en una de las
ecuaciones.
2x-4y+7z=24 (1)
4x+2y-z=4 (2)
3x+3y-z=4 (3)
comenzamos a multiplicar(1) por 2 para hacer de cada coeficiente de
x un múltiplo del primero.
2x-4y+7z=24
4x+2y-z=4
6x+6y-2z=8
después multiplicamos (1) por -2 y le
sumamos el resultado a (2) para eliminar el coeficiente de x en (2)
2x-4y+7z=24
0+10y-17z=-44
6x+6y-2z=8
ahora multiplicamos (1) por -3 y le
sumamos el resultado a (3)
2x-4y+7z=24
0+10y-17z=-44
0+18y-23z=-64
ahora multiplicamos la nueva ecuación
(3) por -5 para hacer que el coeficiente de y sea un múltiplo del coeficiente
de la ecuación (2)
2x-4y+7z=24
0+10y-17z=-44
-90y115z=320
ahora multiplicamos (2) por 9 y le
sumamos el resultado a (3)
2x-4y+7z=24
0+10y-17z=-44
0+0-38z=-76
z=(-76)/(-38)
z=2
ahora empezamos a sustituir z en la anterior así
10y-17(2)=-44
10y-34=-44
10y=-10
y=-1
ahora sustituimos y y z en la primera ecuación así
2x-4(-1)+7(2)=24
2x+4+14=24
2x+18=24
2x=6
x=3
Método
de Determinante por ecuación 3x3.
6x + 3y + 2z = 12
.. 9x - y + 4z = 37
.10x + 5y + 3z = 21
..MATRIZ DE COEFICIENTES
........ | 6 3 .2 | ..
.A. =. | 9 -1 .4 |
........ | 10 5 3 |
................................. | x | ..
matriz de incognitas X = | y | ..
................................. | z | ..
................................... | 12 |
matriz de constantes B = | 37 | ..
................................... | 21 | ..
..
sistema matricial
.... AX = B
Determinante del sistema Det(A)
Toma determinante a la matriz de coeficientes A
..
.................. | 6 .. 3 ..2 | ..
, Det(A) = ... | 9 ..-1 . 4 | ..= 11
.................. | 10 . 5 ..3 | ..
Halla el determinante de"x", Det(A1)
en Det(A) se reemplaza la columna 1
por la columna de las constantes 12,37,21
.................... | 12 ..3 . 2 | ..
, Det(A1) = ... | 37 .-1 . 4 | ..= 55
.................... | 21.. 5 . 3 | ..
Para "y", encuentra Det(A2) que resulta de reemplazar
en Det(A) la columna 2 por la columna B
.................... | 6 . .12 ..2 | ..
, Det(A2) = ... | 9 .. 37 . 4 | ..= -44
.................... | 10 .21 ..3 | ..
Si cambias la columna 3 por la columna B
obtendrás el Det(A3) para la variable "z"
.................... | 6 .. 3 ..12 | ..
, Det(A3) = ... | 9 . -1 . 37 | ..= -33
.................... | 10 . 5 ..21 | ..
Luego la regla de Kramer
x = Det(A1)/Det(A) = 55/11= 5
y = Det(A2)/Det(A) = -44/11= -4
z = Det(A3)/Det(A) = -33/11= -3

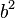 es menor que
es menor que  los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.
los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.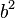 es mayor que
es mayor que  obtendremos dos valores distintos de X reales.
obtendremos dos valores distintos de X reales.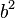 es igual que
es igual que  obtendremos dos valores de X reales e iguales.
obtendremos dos valores de X reales e iguales. se le llama discriminante
se le llama discriminante





















